Beh, conosci la probability density function di una gaussiana:

Quindi la cosa teorica è che ad es. per trovare gli individui attesi tra 49.5 e 50.5 farai l'integrale della pdf fra 49.5 e 50.5 e moltiplichi il risultato per il numero totale di individui
Per fortuna esistono i computer e ad es. con poche linee di codice R ottieni facilmente il risultato (con tanto di plot!)
# Le classi dell'istogramma
classes <- seq(48.5, 58.5, 1.0)
# I valori osservati
observed <- c(4,7,9,10,15,11,10,8,5,2)
# Il numero totale di osservazioni
total <- sum(observed)
# I valori attesi (creiamo un array di zeri)
expected <- array(0, length(observed))
# La media/sd attese
exp.mean <- 52.25
exp.sd <- 2.29
# Passiamo tutte le classi
for (i in 1:length(expected))
{
# La funzione pnorm(x) restituisce la somma cumulativa della pdf (cdf(x))
# ovvero l'integrale fra -Inf e x. Facendo la differenze dei due valori
# di cdf otteniamo l'integrale fra x1 e x2
expected[i] <- (pnorm(classes[i+1], mean=exp.mean, sd=exp.sd) -
pnorm(classes[i], mean=exp.mean, sd=exp.sd)) * total
}
# Il grafico dei risultati!
plot(observed, t="o", col="red", lwd=2, xaxt="n", pch=20)
points(expected, t="o", col="gray", lwd=2, lty=3, pch=20)
legend("topright", c("Osservati", "Attesi"), fill=c("red", "gray"), border=0)
Immagine:
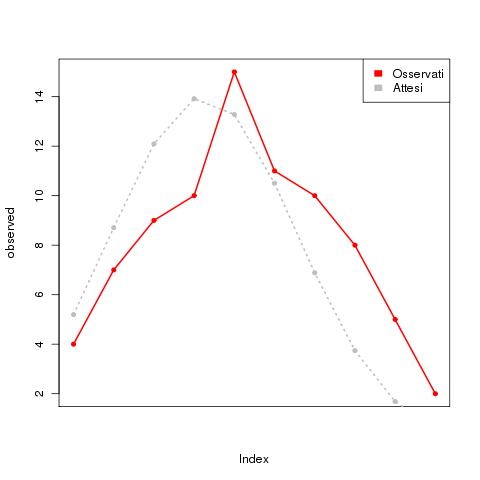
15,85 KB
PS: non ho capito cosa c'entri il chi quadro con questo esercizio...









